Aufgabe A 1.1
Gegeben ist die Funktion f mit f(x)=10x·e-0,5x. Ihr Graph ist K.
a) K besitzt einen Extrempunkt und einen Wendepunkt.
Geben Sie deren Koordinaten an.
Geben Sie eine Gleichung der Asymptote von K an.
Skizzieren Sie K.
(4 VP)
b) Für jedes u>0 sind O(0|0), P(u|0) und Q(u|f(u) ) die Eckpunkte eines Dreiecks.Bestimmen Sie einen Wert für u so, dass dieses Dreieck den Flächeninhalt 8 hat.
Für welchen Wert von u ist das Dreieck OPQ gleichschenklig?
(4 VP)
c) Auf der x-Achse gibt es Intervalle der Länge 3, auf denen die Funktion den Mittelwert 2,2 besitzt.Bestimmen Sie die Grenzen eines solchen Intervalls.
(3 VP)
Aufgabe A 1.2
Gegeben ist für jedes t>0 eine Funktion ft durch
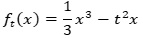 .
.Bestimmen Sie t so, dass die beiden Extrempunkte des Graphen von ft den Abstand 13 voneinander haben.
(4 VP)